强化无线通信滤波效果 连续时间ΔΣ调制器受瞩目
2014年12月15日 15:14 发布者:designapp
连续时间Σ-Δ调制器(Continuous-Time ΔΣ Modulator)先天上具有对输入信号滤波的效果,可降低前级滤波器设计复杂度,并提升信号质量,因而成为现今无线通信系统接收机(Receiver)设计的常用方案。
无线技术目前已广泛应用于人类的生活中,低功率无线收发器(Ultra-Low-Power Wireless Transceiver)更是无线通信电路发展的重要关键。目前接收(Receiver)中的模拟数字转换器(ADC)普遍提出的架构,皆以低通Σ-Δ调制器(Low-pass Delta-Sigma Modulator)为主(图1),信号经过带通滤波器(BPF)、低噪声放大器(LNA),再经由混频器(Mixer)做降频的动作,接着在基带(Baseband)做数字化处理。
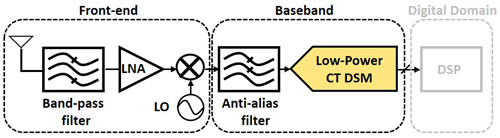
图1 传统接收器架构图
Σ-Δ模拟数字转换器(Delta-Sigma Analog-to-Digital Converter)一直以来是一个可以得到高分辨率(Resolution)的电路架构,其中连续时间Σ-Δ调制器(Continuous-Time Delta-Sigma Modulator, CTDSM)因先天上具有对输入信号滤波的效果,使前级滤波器在设计需求上可以比较宽松,因此CTDSM成为在设计接收机时,常被使用的要素之一。当然此类的ADC设计上有许多地方须要注意,现今仍有诸多文献在这个领域有不少着墨,以致力于低功耗、宽带的CTDSM设计。
本文主要分成两大部分,第一部分为过采样ADC的基本运作原理介绍,第二部分则针对现今文献在CTDSM所提出的技术,做一些简单的介绍。
采样/量化影响ADC信号准确
ADC的运作过程主要分为采样(Sampling)和量化(Quantization)两大步骤。采样的动作是将连续信号转为离散的数据,在此过程中,势必会遇到两个问题,第一是如何确定取得的结果为所需要的信号;第二是要多快的采样频率才够准确。
由频率图(图2)的结果可以发现,第一,为了确保采样信号确实是我们要的,一般会先经过抗混叠滤波器(Anti-Alias Filter)来过滤不要的信号;第二,经过采样后,若信号带宽超过fs/2的话,那数据会互相重迭导致失真发生,如同尼奎斯特准则(Nyqusit-Sample-Theorem)中所述,采样频率至少必须大于两倍数据带宽。
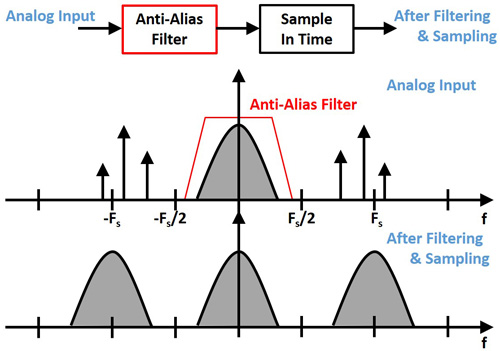
图2 采样频谱图
量化的动作是将连续的振幅转为离散数值,而量化中产生的误差会影响准确度(图3(a)),假设输入的信号为一个三角波(Ramp Signal),则量化误差会呈现锯齿波(图3(b)),并分布在±0.5Δ内(表示Δ量化阶的差值);如果输入没有造成超负荷(Overload),则量化误差可以视为一个均匀分布的函数,其机率密度函数ρ(e)如图4所示,其平均值(Mean Value)为0,量化误差的功率等于其变异值(Variance),可表示为:
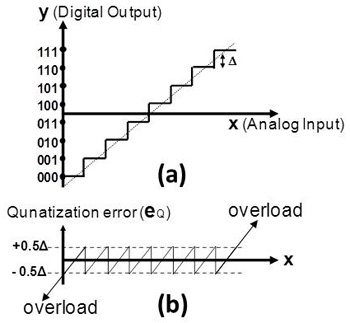
图3 (a)3位的转移函数、虚线为三角波输入,(b)对应之量化误差
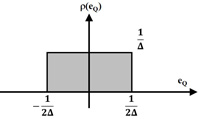
图4 量化误差的机率密度函数
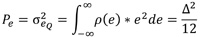
......公式1
接着为了求ADC的信噪比(SNR),必须要知道信号的功率。若输入一个弦波到一个输出为N个位的ADC,在转换器未达超负荷的前提下,输入弦波的最大振幅为A,则A满足:
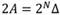
......公式2
所以输入的功率可以表示为:
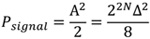
......公式3
因此SNR的最大值可以表示为:
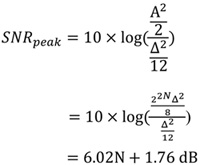
......公式4
根据上述公式,每增加一个位可以增加6dB,所以对于一个高分辨率的ADC,则实际上需要一个N位的输出,这在实作上将难以达成,因此后来提出过采样(Oversampling)的方式来改善这个问题。
搭配噪声整形 过采样可减少误差
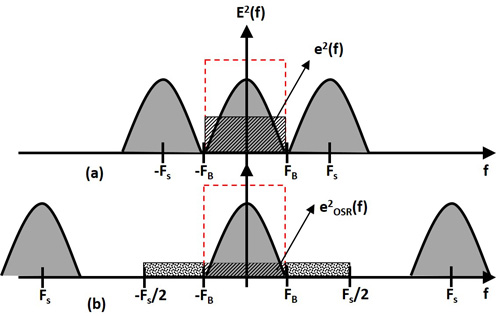
上述在ADC满足采样频率为信号带宽两倍的,属于尼奎斯特型(Nyquist Rate) ADC(图5(a))。过采样的意思即是采样频率大于两倍的带宽,这时候可以定义一个参数是过采样比例(Over-Sampling-Ratio, OSR)为:
1)">
图5 (a)量化误差功率分布(OSR=1),(b)量化误差功率分布(OSR>1)
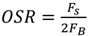
(FB为信号的带宽)............................公式5
假设量化误差为白噪声(White Noise),即它的功率为均匀地分布在Fs/2之间(图6(b)),则它的功率谱密度(Power-Spectral-Density)为:
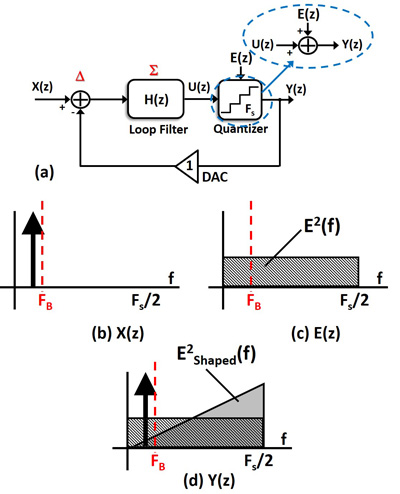
图6 (a)三角积分器示意图;(b)输入X(z)频谱图;(c)量化误差E(z)频谱图;(d)输出Y(z)频谱图
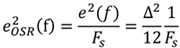
......公式6
则于信号带宽(FB)内的总量化误差功率PNoise,OSR为:
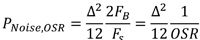
......公式7
因此SNROSR的最大值可以表示为:
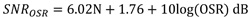
......公式8
由上述公式可以知道,固定信号带宽下,每两倍OSR(即Fs两倍)仅增加3dB(0.5个位)。由结果可以发现,仅增加OSR所获得的好处并不大,因此一般会进一步配合噪声整形(Noise-Shaping)的技巧。
Σ-Δ调制器改善量化误差
三角积分器本身即同时采用过采样及噪声整形两项技巧,噪声整形即利用相减(Delta, Δ)和积分(Sigma, Σ)组合而成(图6(a))。则量化误差E(z)所经过的转移函数(Noise-Transfer-Function, NTF)为:
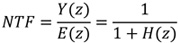
......公式9
则输入信号X(z)所经过的转移函数(Signal-Transfer-Function, STF)为:
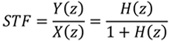
.....公式10
由上面两个公式可以发现,当选择H(z)为一个高直流增益的低通滤波器时,噪声转移函数则为一个高通滤波器函数,代表本来为白噪声分布的量化噪声E(z)会经过高通滤波器塑型;而信号转移函数则为一个低通滤波器函数,代表在低频时,输入信号X(z)经过增益为一的输入转移函数到输出。而同时因为采用过采样,所以信号带宽相对于采样频率小很多,即大部分的量化误差都被塑型到信号带宽(FB)外面,所以带宽内的量化误差被大幅度的减少。
因此,调制器的输出Y(z)包含输入信号即经过塑型的量化误差ESHAPE(z)(图6(b)(c)(d))。最后依据环路滤波器(Loop-Filter)为离散型H(z)或连续型H(s),可分为连续型或离散型Σ-Δ调制器。一个环路滤波器阶数为L的Σ-Δ调制器,其SNRDSM的最大值可以表示为:
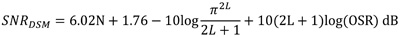
......公式11
由上面公式可以知道,固定信号带宽下,每两倍OSR可以增加(6L+3)dB,假设一个三阶的环路滤波器,则可以增加21dB,相对于只有做过采样,可多得到18dB(三个位)。
低功率CTDSM适用于无线通信系统
以下将针对连续型三角积分器中各个子区块做说明。在过采样Σ-Δ调制器中,架构上可以分成两种形式,一种是离散时间Σ-Δ调制器(Discrete-time Delta-sigma Modulator, DTDSM),另一种则是CTDSM。由于架构先天上的优势,CTDSM比起DTDSM更适用于高速、宽带的应用;但是随着带宽需求的增加,采样频率(Fs)也会随着增加,伴随而来的就是更高的功率消耗,主要可以分几个部分来说明。
首先,因为带宽的增加,使得用来实现CTDSM中环路滤波器的运算放大电路,需要更高的单位增益带宽(Unit Gain Bandwidth),这样的需求也同时伴随着更高的功率消耗;另一方面,因为用于CTDSM中的量化器,是操作在采样频率的速度,因此随着采样频率的增加,也会使得量化器为了达到速度的需求,须要消耗更多的电流来压低运算时间。
在高规格的CTDSM中,为了增加回授路径上之数字模拟转换器(Digital to Analog Converter, DAC)的线性度,常会使用数据加权平均(Data Weighted Averaging, DWA)的方法,来降低DAC中各个单位Cell之间不匹配所造成的Harmonic Tone。
再者,由于整个CTDSM是一个负反馈的闭回路系统,这使得每一笔从量化器输出的数据,都需要在小于一个、甚至是半个采样周期的时间回授到CTDSM的输入,系统才会稳定,也就是整个信号路径包含环路滤波器、量化器以及DWA所贡献的延迟,须要压在半个周期(0.5/Fs)内完成。
当环路滤波器以及量化器都会贡献一定程度上的延迟时,DWA电路就须要操作在更高的速度,使其所贡献的延迟更小,保持CTDSM系统的稳定,但是更高速的操作,就代表需要更多的功率消耗。
最后,就是延迟回路(Excess Loop Delay, ELD)的补偿。因为整个闭回路系统上的电路所贡献的延迟时间,相较于采样频率是不可忽略的,因此这样额外的延迟等效上就是在系统上增加额外的极点,使得系统稳定度下降。
为了补偿这个不理想性,高速的CTDSM通常需要额外的补偿路径,使系统可以正常的操作,而这个额外的补偿路径通常需要额外的DAC甚至是额外的运算放大器来实现信号相加减的运算,这都使得高速CTDSM比起低速的CTDSM,须消耗更多的硬件以及功耗。
但是,如果希望在CTDSM应用于无线通信系统中,功耗就必须压低,基于这样的需求,有许多技术被提出来降低CTDSM中各部分的功率消耗。
基本上CTDSM系统架构可以简单分为几个电路区块,主要的电路区块包含环路滤波器、DAC、量化器(Quantizer)和DWA(图7)。
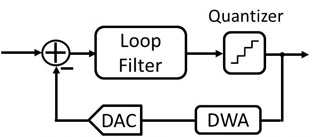
图7 CTDSM基本架构
Gm-C/VCO/Twin-T降低环路滤波器功耗
通常在CTDSM中,如果希望压低量化误差,其中一个方法就是增加环路滤波器的阶数,阶数越高,对带宽内量化误差的压抑效果就越好,但是伴随而来的就是要采用更多的运算放大器来实现积分电路,以达到所需环路滤波器的方程式。
通常积分器的实现都是采用Active-RC架构,环路滤波器的阶数多增加一阶,就须要多增加一个Active-RC电路来实现积分电路;再者,用于Active-RC电路中的运算放大器是属于闭回路应用(Active-RC中的C,通常连接于运算放大器的输入与输出,形成负回授),所以此运算放大器的单位增益带宽必需是采样频率的两到三倍,系统才会稳定。
基于这个考虑,有些高速的应用,就会适当的引入Gm-C架构来实现积分电路,因为Gm-C电路中,Gm的实现是属于开回路的实现方式(Gm的输入与输出点之间并无回授路径),因此对于用来实现Gm电路的单位增益带宽之需求就比较低,也就使得Gm-C的架构可以使用比较少的功耗,实现出相同的环路滤波器转换方程式。
然而,Gm-C的架构因为是开回路架构,所以比起Active-RC的架构,线性度较差,Gm-C架构所贡献的电路噪声也较Active-RC大。因此,Gm-C电路通常只能取代环路滤波器中部分的积分器;而在CTDSM中信号摆伏比较大的地方或是CTDSM的输入端,这些对线性度以及信杂比要求较高,通常还是会采用Active-RC的架构。
Gm-C的架构比起Active-RC架构还有一个缺点,一般Active-RC架构因为是负回授架构,所以会有虚短路(Virtual Short)点可以将输入信号以及回授信号做相加减;但是,因Gm-C电路比较属于开回路架构,并没有明显的虚短路点可以做信号相加减,因此在环路滤波器架构的选取上,比起用Active-RC的方式实现,就会比较受限。
另一方面,为了提升环路滤波器的阶数,同时希望达到低功耗,有些方案会适当的引入电压控制式振荡器(VCO)电路,以同时达到一阶积分效果以及量化的功能。正因为VCO这项将两者功能合而为一的特性,因此能够有效地降低功率消耗。
至于为什么VCO就可以将积分和量化两项功能合而为一,主要是因为VCO在时域上的操作是依据输入电压的不同。VCO电路会振荡在不同的频率,而频率的积分会是相位,因此,只要用一个具有固定相位的信号,和VCO的输出信号做比较,就可以得到VCO在一个采样周期内的相位变化量。等效上就是得到对输入信号积分一个周期后的变化量,这样不但可以使得输入电压因为通过VCO的关系有积分效果,并且输入电压因为VCO也会对应到相位信息。
透过和固定相位的参考频率做比较(通常通过简单的D Flip-Flop就可以实现以及固定频率的频率),可以得到相位是领先或是落后的信息。而得到量化过后的结果,也就是说藉由VCO电路,可以同时实现积分以及量化运算,亦即把积分器以及量化器合而为一,达到降低功耗的目标。
由以下VCO简单的公式推导,可以了解到VCO电路在频域上,的确具有一阶积分的效果:
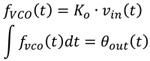
......公式12
Ko:振荡频率的增益
fVCO:VCO的振荡频率
out:VCO的输出相位
Vin:VCO的输入电压(控制电压)
此应用的VCO电路通常使用环形振荡器(Ring Oscillator)(图8),因为环形振荡器可以提供多相位,也就是可以将相位的变化量,区分为更多的状态,等效出多位(多位)量化器的效果,压抑量化误差。然而,因为是采用环形振荡器,压控环形振荡器的线性调变范围很小,因此如果设计不好,很容易产生额外的Harmonic Tone,这是此一架构的缺点。
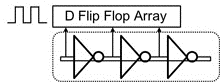
图8 多级环形振荡电路
此外,还有另外一种方法,就是引入双T型滤波器(Twin-T Filter)(图9)。此种滤波器的特性就是可以只使用一颗运算放大器,配合特别设计过的电阻、电容网络,即可得到二阶的积分效果;换句话说,就是T型滤波器的架构可以只使用一颗运算放大器,就能实现出原先需要两个Active-RC积分器才能实现的系统方程式。
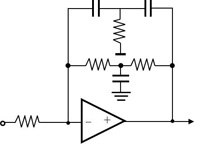
图9 双T型滤波器
很明显的,这个方法可以有效降低运算放大器的使用数量,等效上就是降低环路滤波器的硬件以及功耗。但是这样的方法通常因为只用到一颗运算放大器,就可以实现两阶积分的方程式,比起原先使用两个独立积分器来实现同样的系统方程式,虚短路的点比较少,而使得在系统参数的设系上,会比较受限。设计自由度会比使用两颗单独的运算放大器还低。
综合上述各种架构做一个简单的结论,一般最常见实现环路滤波器的方式是Active-RC架构,但是为了更进一步降低功耗,所以有许多方案会采用Gm-C、VCO-Based、Twin-T等方式实现环路滤波器。图10对环路滤波器的实现方式做了一些简单的结论。
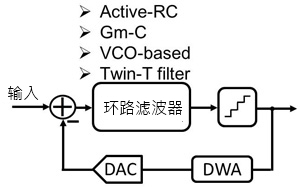
图10 环路滤波器的各种实现方法
DWA处理消除DAC非线性
误差
回授路径上的DAC,如果是使用多位DAC,则DAC的非线性会限制了CTDSM的信号噪声失真比(Signal to Noise and Distortion Ratio, SNDR)。DAC的非线性误差可以被视为一个除了电路噪声以外,额外添加的噪声源,此噪声正是因为DAC中各个子电路(Unit Cell)之间的不匹配。要解决这个问题,最直接的方法就是采用单位元的DAC架构(1Bit DAC),因为只有一个位,就没有所谓不匹配的问题。
但是采用单位元DAC又会衍生其他问题,例如单位元DAC系统中的积分器相较于多位会比较难设计;同时,单位元DAC也对时序信号抖动(Clock Jitter)此一非理想效应更敏感。如果想要使用多位DAC,但是又想要消除非线性度对CTDSM的影响,最常被使用的方式,就是将DAC的输入数字码做适当的处理,也就是所谓DWA的处理。
处理的算法基本方向,就是让不同的DAC Cells平均地被使用。正因为每个DAC Cells都被平均的使用,所以DAC Cells之间的不匹配效应就会受到一定程度的压抑,而使得整体CTDSM可以有更高规格的表现。
一般来说,做这样的信号处理,必须要等到量化器的输出都已经稳定,才可以做进一步的运算。量化器输出经过处理后才会被送到DAC的输入,因而此一电路在回授路径上,也会贡献额外的时间延迟,使系统容易振荡,所以在估计整个CTDSM的系统稳定度时,须要将此一电路所贡献的延迟适当地考虑进去。
在DAC电路上,最适合用于高速的架构莫过于电流导引(Current Steering)。DAC设计上,最大的问题除了线性度以外(通常会配合DWA电路加以解决),另外就是电路热噪声的问题。目前面对电路噪声问题,最好的解决方法就是拉高DAC电源电压,使热噪声可以降低,此外鲜少有比较好的解决方法。
本篇文章分为主要两个部分,在第一部分,介绍了DSM基本的架构以及操作原理,包含过采样(Oversampling)、噪声整形(Noise Shaping)等概念;第二部分则是更进一步介绍了CTDSM各部分子区块的电路架构,包含环路滤波器、量化器、DWA电路以及ADC。针对各个部分,本文亦介绍了许多现今常被使用的技术以及其优缺点。
